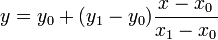I chose this piece because it aims to explain the complexity of group theory in more basic terms. I believe that I communicated this branch of math in a way that non-math majors would even grasp the ideas.
In this writing I let a simple curiosity lead into a full-out study of the historical method of elchataym used by Fibonacci. Although I left it open at the end (and would have built a stronger piece if time permitted), I still exhibited my understanding of a very influential part of math's history. When we explored Fibonacci's Liber Abaci on Thursday, I was intrigued by chapter 13: On the Method Elchataym and How with It Nearly All Problems of Mathematics Are Solved. What a title! I couldn't stop wondering about this mysterious method of elchataym and how it could possibly be so universal. I read through a translated snippet of the chapter online and also studied some articles which discuss elchataym in modern math terms. Elchataym comes from the Arabic "al-khata'ayn", meaning "the two errors". In Liber Abaci, Fibonacci introduces elchataym as "the method of double false position". This method was first used before his time by Chinese and Arab mathematicians. Fibonacci's description of the method went right over my head, each of the eight times that I read it. I decided to start with the basics and find out what double false position actually means. It seems that elchataym is a form of "guess and check". An article titled "False Position in Leonardo of Pisa's Liber Abbaci" by John Hannah (University of Canterbury, New Zealand) says that to use double false position, "Leonardo uses two guesses at the value of the unknown, and then compares them to see how much closer he is to the target value" (Hannah 11). Fibonacci seems to approximate his answers by adjusting the values for x and y until he reaches the number he is looking for (or one very close to it). A quote from the translation of chapter 13 of Liber Abaci shows Fibonacci's thought process regarding elchataym: “For the one pound that I increased in the second position, I approached more closely to the true value by 3 ounces of silver. How much should I increase the second position so that I approach more closely by another 3 ounces?” Multiple sources defined double false position as a method that we now call linear interpolation. This term was also new to me, so I researched it. Wikipedia defines linear interpolation as "a method of curve fitting using linear polynomials." This definition opened my eyes a bit. I read on to find out that for two known points with coordinates (x0,y0) and (x1,y1), the formula for linear interpolation is This writing will be left open-ended because I need to do further research in order to gain a better understanding of elchataym and all of its wonder.
Sources: http://en.wikipedia.org/wiki/Linear_interpolation http://link.springer.com/chapter/10.1007%2F978-1-4613-0079-3_14# http://en.wikipedia.org/wiki/False_position_method "False Position in Leonardo of Pisa's Liber Abbaci", John Hannah (University of Canterbury, New Zealand) I spent a lot of time working and learning on Desmos and was able to observe (known and unknown) graphic results based on the equations that I tried out. By explaining my process below, I not only did the hands-on math, but also organized my thoughts enough to put them into easy-to-follow words.
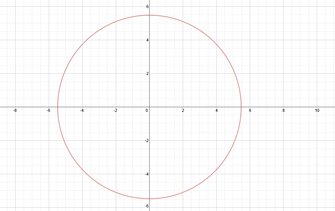
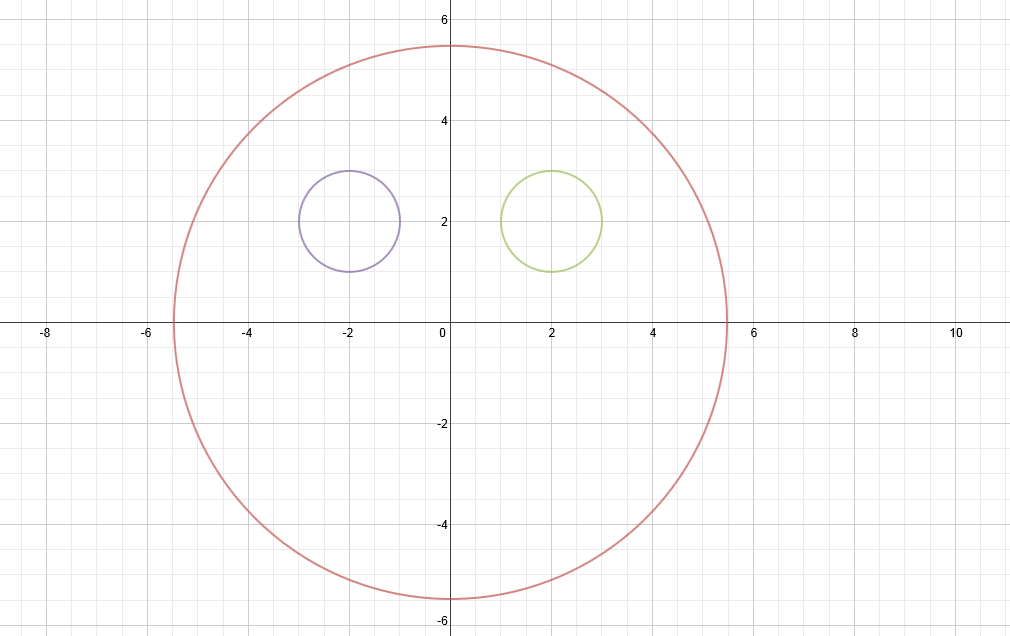
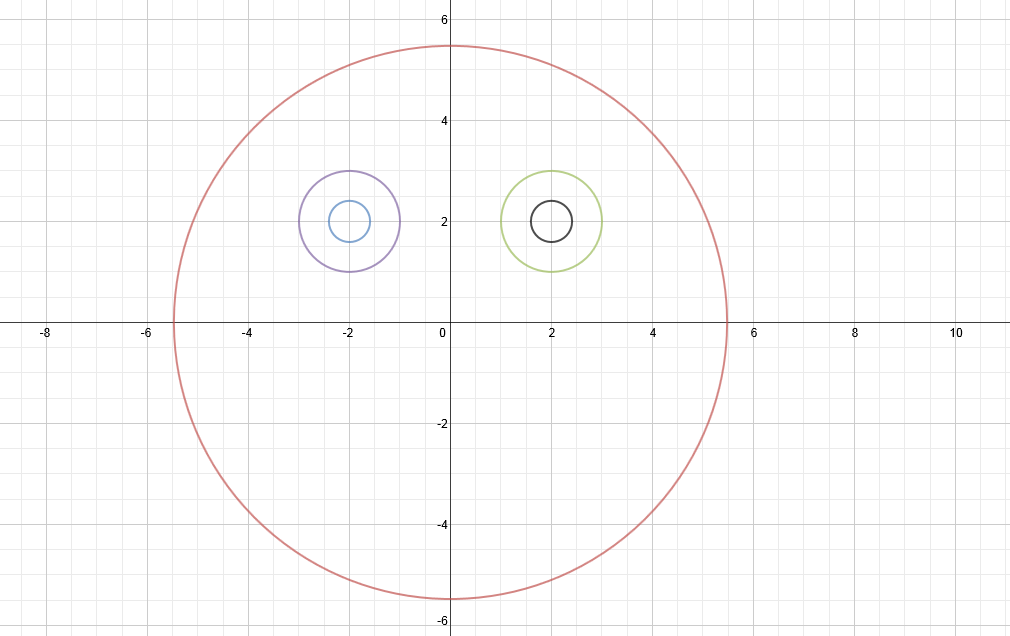
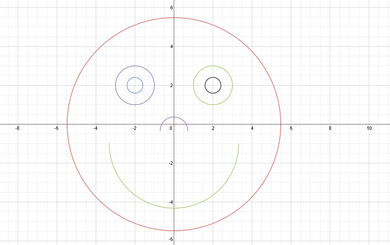
This week I decided to work on the "Doing Math" category of weekly work. After learning about Desmos and Daily Desmos in class, I started to play around on the site. This was time well spent, since I have not done legitimate graphing of equations in years. I also came to realize that graphic results of equations never really stuck with me (i.e. the effects of the type of equations, shifting/rotating of graphs, etc.) when I learned about them previously, so I found myself learning several new things and even having fun while doing it. This post will outline the process that I followed in order to create the graph of a familiar symbol and lessons that I learned (and re-learned) along the way. When I opened Desmos and began to explore, one that came to my mind was, "I wonder if I can make a smiley face graph." It seemed simple enough to just put together circles and arcs. I remembered that the equation for a circle was x^2+y^2=b, so I started there. Using that equation and a bit of shifting and value changing, the head and eyes were a breeze to create. In order to create the left eye, I subtracted from x and shifted it horizontally. I added to the x value in order to create the left eye. Moving the eyes toward the top of the face was done by subtracting from the y value that was being squared. Using the same numerical values for the eyes (and only changing a sign) assured their symmetry. To make the face more detailed, I decided to add "pupils". In order to do so, I used equations identical to those for the eyes but made the b value much smaller. This resulted in the "pupils" having the same center as the eyes but being placed inside of them. Equation for: -head: x^2+y^2=30 -left eye: (x+2)^2+(y-2)^2=1 -right eye: (x-2)^2+(y-2)^2=1 -left pupil: (x+2)^2+(y-2)^2=1/6 -right pupil: (x-2)^2+(y-2)^2=1/6 Next I thought about making the nose and mouth. I knew that I wanted to form arcs. I naively tried a few equations, including 1/2 times the equaton for a circle. No luck with that or the others. I ended up looking online to find out what type of equation would make an arc. I found that equations of the form sqrt(b-x^2) would work. So I felt my way around in Desmos and eventually formulated appropriate equations to fit into my smiley face as its nose and mouth. The only main difference between these features (besides size, which depended on b) is their orientation, which I set with a simple sign change at the beginning. Equation for: -nose: sqrt(1/2 - x^2) - 1/3 -mouth: -sqrt(11-x^2)-1 The step-by-step pictures of my creation as well as the final result are shown below. I chose this writing because I outlined one of the most essential components of math, axioms, in a clear and detailed way. I learned new information and was able to form a solid understanding of axioms through my research.
An axiom is a statement that is accepted as true without proof. Axioms form the basis of mathematical proofs that are written in order to establish theorems. In order to formally prove conjectures, we must start with given information. Axioms often supply us with this assumed information. There are two major roles that axioms play in mathematics. 1. They describe undefined terms (line, point, etc.). 2. They provide us with a starting point to prove conjectures. The Greeks (and majorly Euclid) are known for first using mathematical axioms over 2000 years ago. Their axiomatic approach involved undefined objects such as points and lines. These axioms are simple forms of statements which cannot be further broken down without philosophical considerations. The axioms that I am most familiar with are those within Euclidean geometry. Euclid’s famous bookThe Elements contains his geometric axioms. Axioms are sometimes organized into systems, as Euclid's were. An axiomatic system is a collection of axioms such that each axiom is independent from the others – that is, no axiom can be proven from any other axiom in the set. In Euclidean geometry there is a system of five essential postulates (which are synonymous to axioms) called Euclid's Postulates. These postulates are the building blocks which are used to prove every theorem of Euclidean geometry. They are: 1. A straight line segment can be drawn joining any two points. 2. Any straight line segment can be extended indefinitely in a straight line. 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. 4. All right angles are congruent. 5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. Euclid also wrote a set of "Common Notions", which are axioms that go beyond geometry and refer to general logic. These notions are: 1. Things which are equal to the same thing are also equal to one another. 2. If equals be added to equals, the wholes are equal. 3. If equals be subtracted from equals, the remainders are equal. 4. Things which coincide with one another are equal to one another. 5. The whole is greater than the part. Euclid's axiomatic writing was widely accepted and stable for thousands of years. Then, in the 19th century, mathematicians Ivanovitch Lobachevski, Karl Gauss, and János Bolyai extensively studied Euclid's Postulates and attempted to find contradictions within them. Instead, these men ended up creating non-Euclidean, hyperbolic geometry. In the 20th century, Albert Einstein referenced hyberbolic geometry to write The General Theory of Relativity. It is evident that axioms (especially Euclid's) are the foundation of mathematical theory and have remained meaningful for over 2,000 years of mathematical discovery. Without axioms, math would not have developed into the beautiful science that it is today! |