This week I decided to work on the "Doing Math" category of weekly work. After learning about Desmos and Daily Desmos in class, I started to play around on the site. This was time well spent, since I have not done legitimate graphing of equations in years. I also came to realize that graphic results of equations never really stuck with me (i.e. the effects of the type of equations, shifting/rotating of graphs, etc.) when I learned about them previously, so I found myself learning several new things and even having fun while doing it. This post will outline the process that I followed in order to create the graph of a familiar symbol and lessons that I learned (and re-learned) along the way.
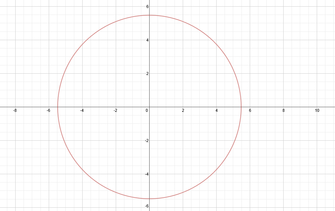
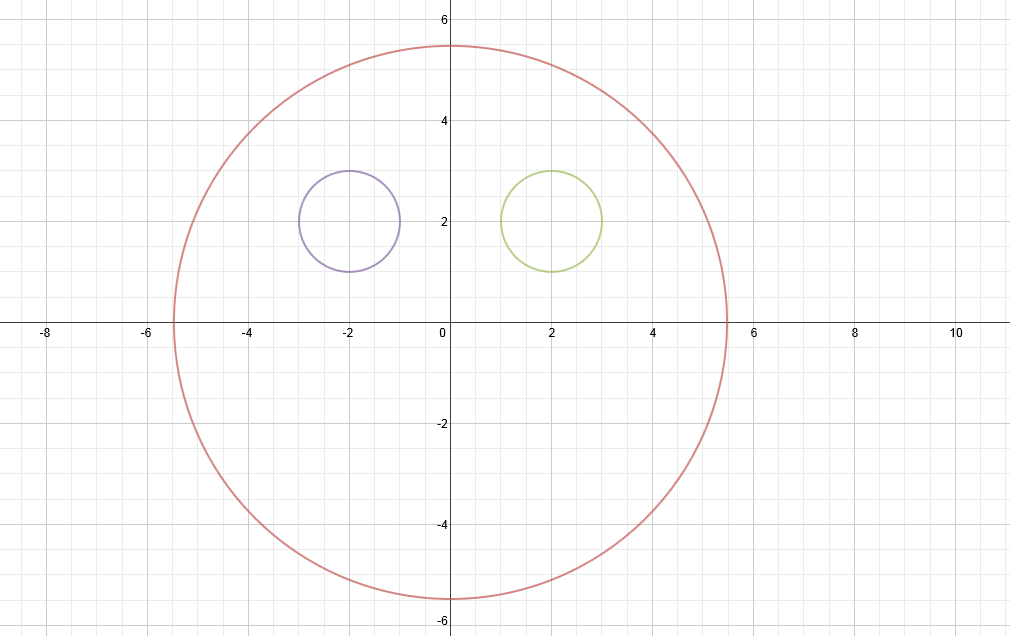
When I opened Desmos and began to explore, one that came to my mind was, "I wonder if I can make a smiley face graph." It seemed simple enough to just put together circles and arcs. I remembered that the equation for a circle was x^2+y^2=b, so I started there. Using that equation and a bit of shifting and value changing, the head and eyes were a breeze to create. In order to create the left eye, I subtracted from x and shifted it horizontally. I added to the x value in order to create the left eye. Moving the eyes toward the top of the face was done by subtracting from the y value that was being squared. Using the same numerical values for the eyes (and only changing a sign) assured their symmetry.
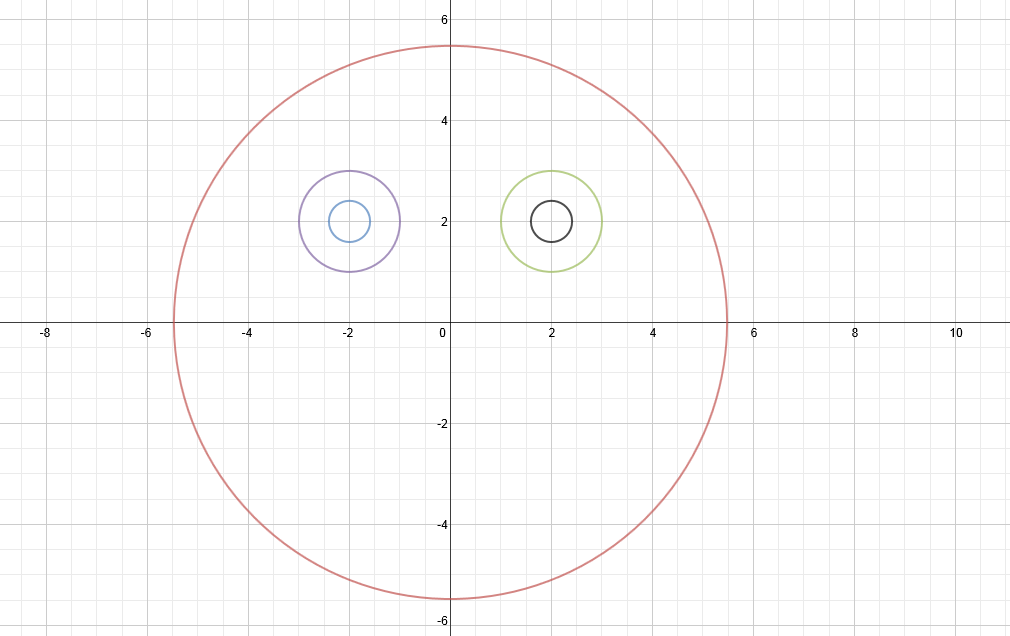
To make the face more detailed, I decided to add "pupils". In order to do so, I used equations identical to those for the eyes but made the b value much smaller. This resulted in the "pupils" having the same center as the eyes but being placed inside of them.
Equation for:
-head: x^2+y^2=30
-left eye: (x+2)^2+(y-2)^2=1
-right eye: (x-2)^2+(y-2)^2=1
-left pupil: (x+2)^2+(y-2)^2=1/6
-right pupil: (x-2)^2+(y-2)^2=1/6
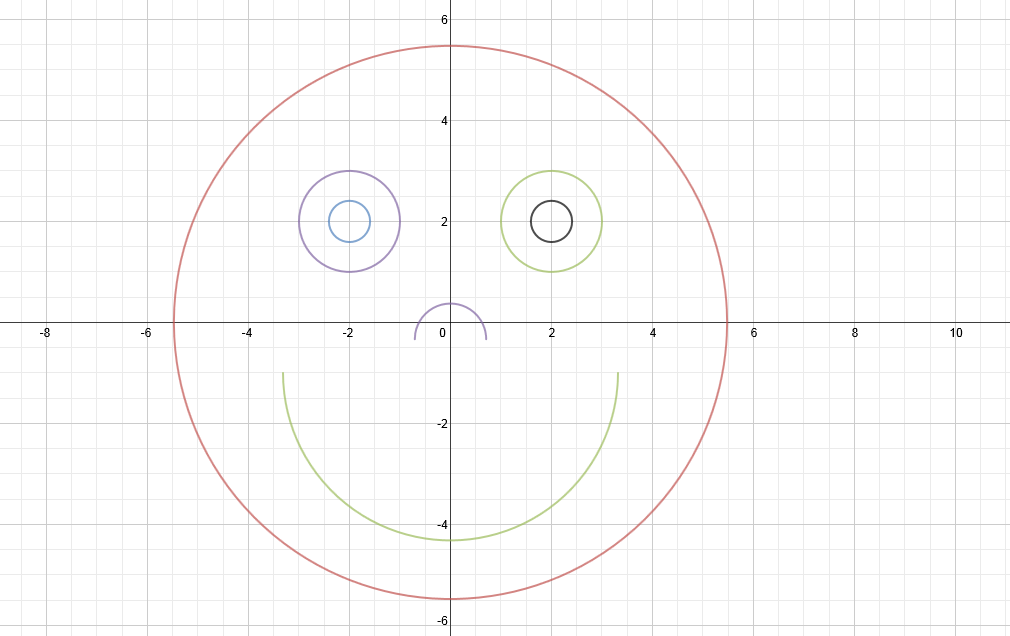
Next I thought about making the nose and mouth. I knew that I wanted to form arcs. I naively tried a few equations, including 1/2 times the equaton for a circle. No luck with that or the others. I ended up looking online to find out what type of equation would make an arc. I found that equations of the form sqrt(b-x^2) would work. So I felt my way around in Desmos and eventually formulated appropriate equations to fit into my smiley face as its nose and mouth. The only main difference between these features (besides size, which depended on b) is their orientation, which I set with a simple sign change at the beginning.
Equation for:
-nose: sqrt(1/2 - x^2) - 1/3
-mouth: -sqrt(11-x^2)-1
The step-by-step pictures of my creation as well as the final result are shown below.
When I opened Desmos and began to explore, one that came to my mind was, "I wonder if I can make a smiley face graph." It seemed simple enough to just put together circles and arcs. I remembered that the equation for a circle was x^2+y^2=b, so I started there. Using that equation and a bit of shifting and value changing, the head and eyes were a breeze to create. In order to create the left eye, I subtracted from x and shifted it horizontally. I added to the x value in order to create the left eye. Moving the eyes toward the top of the face was done by subtracting from the y value that was being squared. Using the same numerical values for the eyes (and only changing a sign) assured their symmetry.
To make the face more detailed, I decided to add "pupils". In order to do so, I used equations identical to those for the eyes but made the b value much smaller. This resulted in the "pupils" having the same center as the eyes but being placed inside of them.
Equation for:
-head: x^2+y^2=30
-left eye: (x+2)^2+(y-2)^2=1
-right eye: (x-2)^2+(y-2)^2=1
-left pupil: (x+2)^2+(y-2)^2=1/6
-right pupil: (x-2)^2+(y-2)^2=1/6
Next I thought about making the nose and mouth. I knew that I wanted to form arcs. I naively tried a few equations, including 1/2 times the equaton for a circle. No luck with that or the others. I ended up looking online to find out what type of equation would make an arc. I found that equations of the form sqrt(b-x^2) would work. So I felt my way around in Desmos and eventually formulated appropriate equations to fit into my smiley face as its nose and mouth. The only main difference between these features (besides size, which depended on b) is their orientation, which I set with a simple sign change at the beginning.
Equation for:
-nose: sqrt(1/2 - x^2) - 1/3
-mouth: -sqrt(11-x^2)-1
The step-by-step pictures of my creation as well as the final result are shown below.